How to calculate the self weight of the different structural elements

A building load belongs to a force that should be confronted by the house frame. The frame should be designed in an efficient manner to resist eight of these loads ranging from wind, earth, and snow devoid of catastrophic stress on the structure.
Given below, the detail calculation method of self weight for the structural components:
a. Beam: It is applicable to different types of shapes like rectangular/square/tee/trapezoid for measuring the weight.
Weight of member = cross section area of member x length of member x RCC density
Suppose, the width is taken as 0.3 m and depth is taken as 0.45 m for the beam section with 5 m clear length & material density = 25 kn/m3 (for RCC), the weight should be as follow :-
Weight of beam = (0.3 x 0.45) x 5 x 25 = 16.875 Kn
The above calculated weight of 16.875 Kn stands for the total weight that should be transformed into Uniformly Distributed Load (UDL) by dividing the total weight with member length.
UDL = 16.875/5 = 3.375 Kn/m
b. Column: While measuring the self-weight of a column, the terminology of member length should be converted to member height & the weight of column should be computed as point load only its conversion in UDL is not necessary.
c. Slab: For RCC slabs, the weight of roof slabs is employed as invariable pressure in Kn/m2. For making analysis, a 1 m x 1 m square section is taken into consideration & the volume of the RCC is measured & then the same is multiplied with the density for derivation of pressure in kn/m2.
Weight of slab = (1 x 1 x slab thickness) x RCC density
In the above formula as (1 x 1) doesn?t impact the estimate thus it can be further clarified as follow :-
Weight of slab = slab thickness x RCC density
If the thickness of the slab is 0.15 m, then the estimate is done as follows :-
Weight of slab = 0.15 x 25 = 3.75 Kn/m2
In the above estimate of RCC slab weight further supplementary load resulting from floor finishes should be generally taken into consideration for stone/cement floorings as 0.75 kn/m2 to 1.5 kn/m2.
The U-value unit is the inverse those of R-value:
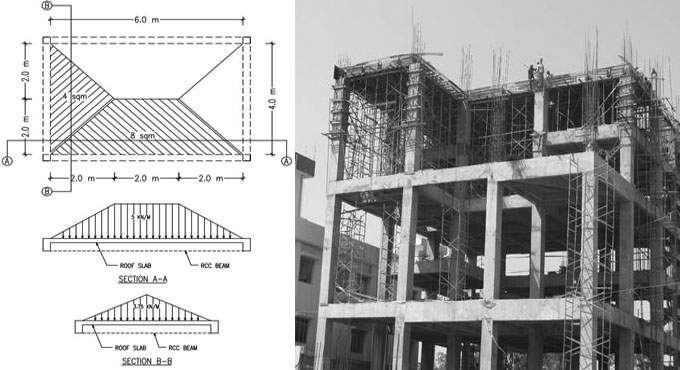
Disposition of slab load on supporting beams: Based on the placement of the beams (square or rectangular) triangular or trapezoidal shape distribution is performed. As for instance, for a rectangular slab of 6 m x 4 m the longer side beams distancing among A-B & D-C will bear the load of related trapezoidal portion while the shorter span beams distancing among A-D & B-C will support weight of roof slab arise out of the related triangular region.
Load on 6 m span = area of trapezoid x thickness of slab x density
Load on 6 m span = 8 x 0.15 x 25 = 30 Kn = 30 / member length = 30/6 = 5 Kn/m
The above estimated load of 30 Kn can be again transformed to UDL of 5 kn/m by dividing it with member length.
Load on 4 m span = area of triangle x thickness of slab x density
Load on 4 m span = 4 x 0.15 x 25 = 15 Kn = 15 / member length = 15/4 = 3.75 Kn/m
To get more details, go through the following article civilengineeronline99.blogspot.com