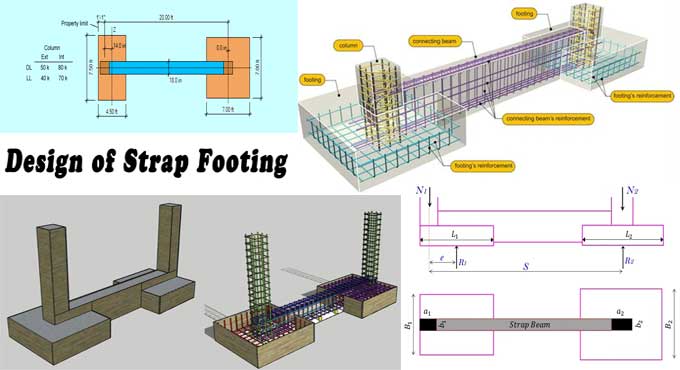
How to Design and Calculate Strap Footing

An integrated footing is designed when two columns are reasonably close to each other. An eccentric moment is transferred between two columns when they are far apart by a strap. It is important to minimize variance in the settlement between columns and to seek uniform bearing pressure.
Design Procedure of Strap Footing
Straps are incapable of bearing weight. Its ridges permit the moment to go from one footing to the other.
Strap Footing Structural Analysis
A. Factored column loads should be calculated for Pua & Pub.
B. Substitute Mu for Pua*e in the eccentric moment equation.
C. Vu = Mu / L = factored shear.
D. Calculate factored reactions, Rub & Rua.
E. Calculate the factored reaction of the footings.
F. Assess the structural integrity of footings and straps by factoring in shear and moment forces.
Service Load Design
A. Measure the length and eccentricity of the footings.
B. Calculate eccentricity, M = PA*e.
C. Calculate the Shear force, V = M / L.
D. Rb = Pb-V; Ra = Pa+V; calculate footing reaction.
E. Size both A & B's footings.
Reinforced Design of Concrete
Conceive a flexural reinforcement for the exterior footing and check for shear stresses. Design interior footings to accommodate shear stresses and reinforce flexural elements. Use footing straps to reinforce concrete beams.
Determine Moment & Shear in a Strap Footing
Data Requirement: The footings and straps should be sized to achieve the maximum factored shear and moment.
Solution
1. The column load of A is 1.4*50 + 1.7*40 = 138 Kips.
2. Loading B by factoring 1.4*100+1.7*80 equals 276 Kips.
3. Mu = 138*2=276 ft-kips factored eccentric moment.
4. A factored shear is equal to 276/20=13.8 Kips.
5. The factored footing reaction is at A = 138+13.8=151.8 Kips.
6. The factored footing pressure of A is 151.8/6=25.3 k/ft.
7. At B = 276-13.8=262.2 kips, the footing reaction is factored.
8. At B, the factored footing pressure per linear foot is 262.2/8=32.8 k/ft.
Moment
The result is -40.5 feet-kips when Mu = 25.3*1.52/2-138*0.5.
A Mu of 25.3*62/2-138*5 is -234.6 feet-Kips.
The Mu factor is 25.3*6*(6/2+13)-138*(5+13) =-55.2 ft-Kips.
The equation for Mu is 25.3*6*(6/2+13+3.5)-138*(5+13+3.5) + 32.8*3.52/2 = 194 ft-Kips.
Shear
The value of vu is 25.3*1.5-138 = -100.1 Kips
The value of Vu is 25.3*6-138=13.8 Kips.
A value of 13.8+32.8*3.5 is equivalent to 128.6 Kips.
A Vu of 32.8*-3.5 equals 114.8 Kips.
Determine Strap Footing Sizes
Data Requirement - Information of Footing
3000 per square foot is the amount of soil that can be loaded. A footing is 1 ft from column A. There is an allowance for 3000 pounds per square foot of soil. There is 120 pounds of soil above the footing. The footing is 24" deep. Above the footing, the soil is 12" deep. Determine the length, width, and depth of footings A & B.
Information of Column
Column A: live load equals 40 kips, dead load equals 50 kips
Column B: The live load equals 80 kips while the dead load equals 100 kips.
are 22 feet between the two columns.
Solution
Footing A has an eccentricity of e = 6/2-1=2' for a width of 6 ft.
Footing reaction distance is based on L = 22 - 2 = 20'
Using (40 + 50)*2=180 feet-kips, you obtain the eccentric moment (M).
To learn more, watch the following video tutorial.
Video Source: Civil Construction And Tutor
M produces shear with V = 180/20=9 kip
footing A, rate of reaction is 40+50+9 = 99 kip
In the net soil bearing capacity formula, 3000-2*150-120=2580 plant square feet
An area of A of 37.4 ft2 is required for the footings.
Using 6' by 6.5' footings, 39 ft2 of area is required.
100 plus 80 + 9 = 171 kip reaction at footing B
171/2.58 = 66.3 ft2 is the area necessary for footings.
Footings should be 8' by 8.5', A = 68 ft2.
Read More
Different types of foundation and their usefulness
Types of footings with diagrams